therealbeda
Level-1
- Beiträge
- 15
- Reaktionspunkte
- 1
-> Hier kostenlos registrieren
Hallo Zusammen,
Ich bin mir nicht ganz sicher ob das das richtige Forum ist für mein Problem, falls nicht, bitte erschlagt mich nicht
Ich habe mich bereits in einem anderen Thread zu Wort gemeldet, da ich derzeit den SPS Kurs der Fernschule Weber belege (aktueller Stand: Hausaufgaben LB1).
Nun stellt sich mir eine Aufgabe bei der ich einen Tipp brauchen könnte:
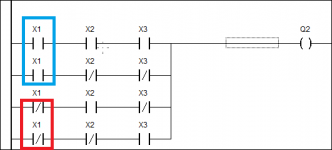
Es soll eine Logik entworfen werden, mit der ein boolesches Ausgangssignal Y den Wert 1 annimmt, wenn eine ungerade Anzahl der Eingänge X1, X2 und X3 den Wert 1 annimmt.
..Hört sich für mich nach einer einfachen Kreuzschaltung an, demnach lautet die Schaltfunktion:
Y = (~X1 * ~X2 * X3) + (~X1 * X2 * ~X3) + (X1 * ~X2 * ~X3) + (X1 * X2 * X3)
zur Erklärung: ~ ist NICHT, * ist UND, + ist oder
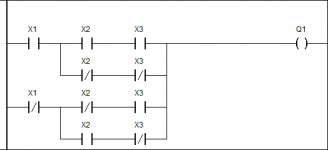
soweit so gut.. die nächste Aufgabe besagt nun ich soll die Funktion mit der booleschen Algebra so kürzen, dass nachher im KOP nur noch 10 anstatt 12 Kontakte übrig bleiben.
Ich rechne seit Tagen rum und habe einige Freunde vom Fach gefragt, es scheint als ist es unmöglich. SOLLTE es tatsächlich eine Kreuzschaltung sein, dann ist es sogar unmöglich (laut wikipedia).
Ich vermute, dass mir irgendwo ein Fehler unterlaufen ist.
Kann mir jemand einen Tipp geben?
Danke
Ich bin mir nicht ganz sicher ob das das richtige Forum ist für mein Problem, falls nicht, bitte erschlagt mich nicht
Ich habe mich bereits in einem anderen Thread zu Wort gemeldet, da ich derzeit den SPS Kurs der Fernschule Weber belege (aktueller Stand: Hausaufgaben LB1).
Nun stellt sich mir eine Aufgabe bei der ich einen Tipp brauchen könnte:
Es soll eine Logik entworfen werden, mit der ein boolesches Ausgangssignal Y den Wert 1 annimmt, wenn eine ungerade Anzahl der Eingänge X1, X2 und X3 den Wert 1 annimmt.
..Hört sich für mich nach einer einfachen Kreuzschaltung an, demnach lautet die Schaltfunktion:
Y = (~X1 * ~X2 * X3) + (~X1 * X2 * ~X3) + (X1 * ~X2 * ~X3) + (X1 * X2 * X3)
zur Erklärung: ~ ist NICHT, * ist UND, + ist oder
soweit so gut.. die nächste Aufgabe besagt nun ich soll die Funktion mit der booleschen Algebra so kürzen, dass nachher im KOP nur noch 10 anstatt 12 Kontakte übrig bleiben.
Ich rechne seit Tagen rum und habe einige Freunde vom Fach gefragt, es scheint als ist es unmöglich. SOLLTE es tatsächlich eine Kreuzschaltung sein, dann ist es sogar unmöglich (laut wikipedia).
Ich vermute, dass mir irgendwo ein Fehler unterlaufen ist.
Kann mir jemand einen Tipp geben?
Danke